電壓探頭關鍵因素對高頻暫態(tài)電壓測量精度的影響分析

仿真電路

高頻暫態(tài)電壓由圖6a所示的雙脈沖測試電路產生，采用Saber軟件進行電路仿真，仿真波形如圖6b所示。所用開關器件為有開爾文源的MOSFET，在各目標信號中，VGs1為高共模電壓低壓差分信號，VDs1為高共模電壓高壓差分信號，VGs2為低共模電壓低壓差分信號，VDS2為高壓對地信號。根據信號類型，VGs1、VDs1和 VGs2需采用差分探頭測量，VDS2既可采用高阻無源探頭測量，也可采用差分探頭測量。當開關器件無開爾文源時，S2驅動回路源端接地，VGs2也可采用高阻無源探頭或具有寬輸入范圍的有源單端探頭測量。

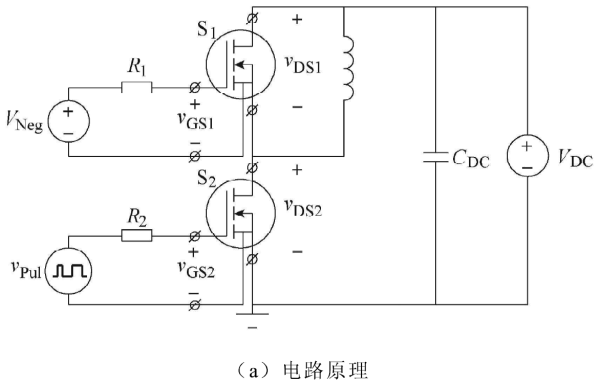
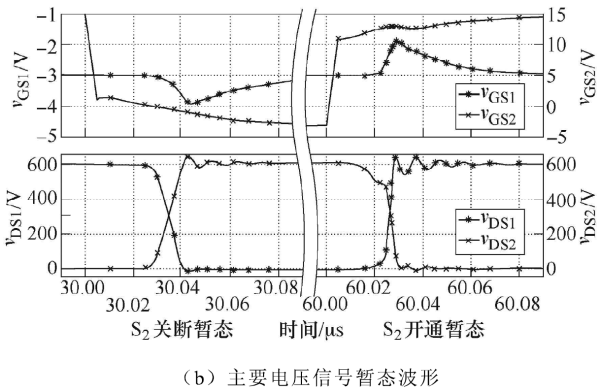
圖6. 雙脈沖測試電路及其仿真結果

帶寬與上升時間

對于n個模塊級聯而成的線性時不變系統(tǒng)，記各級階躍響應的上升時間為tr,m，當各級的階躍響應皆為高斯函數（高斯響應）時，系統(tǒng)的上升時間可表示為

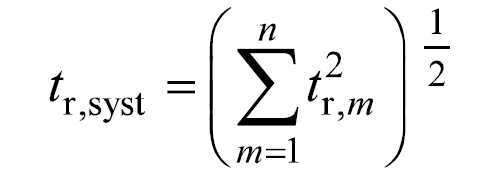
當各級階躍響應有過沖現象且過沖幅度大約為階躍幅度的5%或10%時，系統(tǒng)的上升時間將比式(4)給出的上升時間略短，系統(tǒng)的過沖幅度約為各級過沖幅度總和的二次方根。

考慮目標信號、電壓探頭和示波器級聯形成的系統(tǒng)，各級階躍響應的上升時間依次記為 tr,sign、tr,probe、 tr,scope。其中后兩級組成的測量系統(tǒng)通過示波器的前端放大器相互隔離，使得這兩者的上升時間相互獨立，常用的電壓探頭和示波器一般具有高斯響應，由式(4)可得測量系統(tǒng)的上升時間為

進一步地假設目標信號和電壓探頭的上升時間也相互獨立，則整個系統(tǒng)的上升時間，即示波器顯示波形的上升時間為

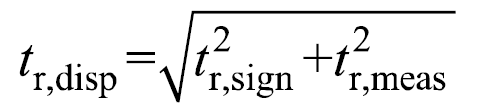
實際上電壓探頭對目標信號有負載效應，目標信號的上升時間將因探頭的加入而改變。負載效應模型如圖7所示。圖中，Vs為單位階躍信號源，Rs為信號源電阻，Cs為負載電容，Vsign為目標信號，Ri與Ci為電壓探頭的輸入阻抗。未施加探頭時，由RC電路的階躍響應函數易得目標信號的上升時間tr,sign為2.2RsCs。同理施加電壓探頭后，目標信號的上升時間變?yōu)?.2(Rs//Ri)(Cs+Ci)。目標信號上升時間因電壓探頭的負載效應而變化的程度可表示為

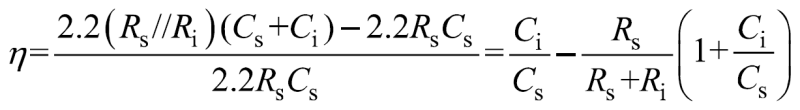
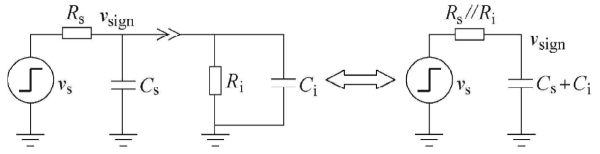
圖7. 電壓探頭對目標信號的負載效應模型

開關器件的柵源電壓和漏源電壓對應的等效負載電容Cs可分別用器件的輸入電容和輸出電容近似，tr,sign可由數據表直接讀出，因此開關器件等效信號源電阻Rs可表示為tr,sign/(2.2Cs)，取現有商售SiC器件進行估算，可得目標信號的等效負載電阻約在100Ω的數量級上,而常用的高阻無源探頭和有源高壓差分探頭的輸入電阻數量級約為MΩ，于是，式(7)可近似為

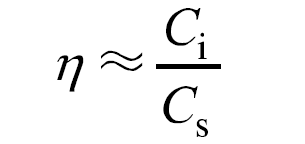
高阻電壓探頭的輸入電容越大，其對開關器件的負載效應越明顯。然而，由于開關器件的輸入電容和輸出電容是變量，不能用式(8)來準確計算。

考慮到電壓探頭的負載效應，式(8)可修正為

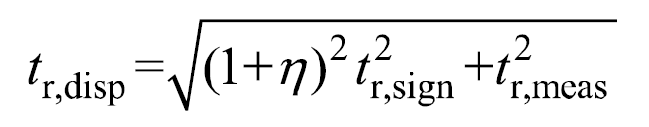
進而可定義測量系統(tǒng)產生的上升時間誤差為

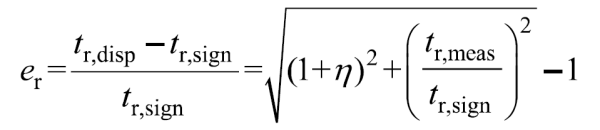
可知，為減小目標信號的上升時間測量誤差，應使電壓探頭的輸入電容足夠小，并且使測量系統(tǒng)的上升時間遠小于目標信號的上升時間。

帶寬和上升時間成反比，對于高斯響應型的測量系統(tǒng)，兩者間關系可近似表示為

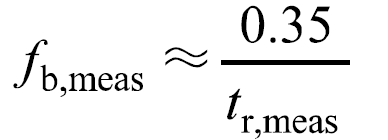
暫態(tài)信號含有豐富的頻率分量，理論上需要用全部的頻率分量才能重構暫態(tài)信號，實際上頻率過高的分量對暫態(tài)信號的重構影響甚微，為此定義拐點頻率，在暫態(tài)信號重構過程，高于拐點頻率的分量將被舍棄。對于目標信號，其拐點頻率表示為

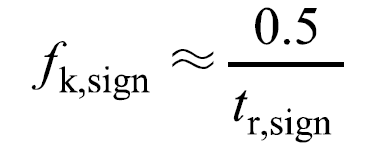
因此，從頻域的角度看，為減小目標信號上升時間的測量誤差，應當要求測量系統(tǒng)的帶寬遠大于目標信號的拐點頻率。

圖8比較了在不同的探頭帶寬下VDs2和VGs2的仿真波形，為簡化分析，不考慮示波器的作用，以探頭輸出電壓Vp和衰減系數k的乘積作為目標信號的測量結果。不難看出，隨著探頭帶寬的降低，目標信號測量結果的上升時間變長，測量誤差也相應增大。此外，可以看出探頭的測量結果滯后于目標信號，即出現傳輸延遲現象，這主要是探頭的傳輸線導致的，本文對此不作深入討論。

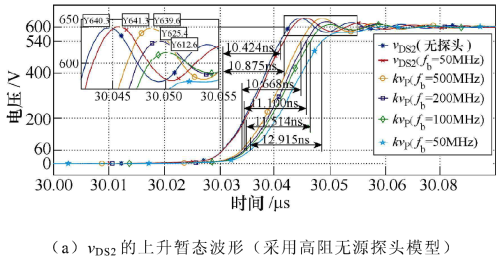
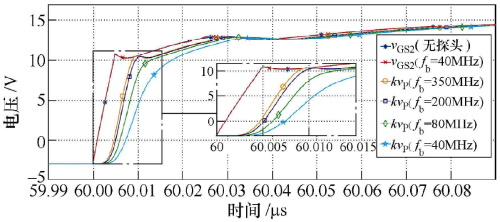
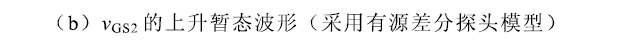
圖8. 不同的探頭帶寬下VDs2和VGs2的仿真波形比較

為定量說明電壓探頭對目標信號測量結果上升時間的作用，取VDs2在50MHz帶寬探頭作用前后的上升時間來分析。由圖8a可知，該探頭的負載效應使VDs2的上升時間由10.424ns變?yōu)?0.875ns，又由式(11)可得該探頭的上升時間約為7ns，將這些數據代入到式(9)可解得探頭測量結果的上升時間為12.933ns，這與仿真得到的12.915ns一致。由式(10)可得，50MHz帶寬探頭對VDs2上升時間的測量誤差達到23.9%，這表明低帶寬探頭無法滿足高頻暫態(tài)信號上升時間的測量要求。

電壓探頭帶寬過低，意味著暫態(tài)信號的高頻分量被極大衰減，當暫態(tài)信號波形具有高頻振蕩或尖刺時，低帶寬電壓探頭將無法還原其快速變化的細節(jié)，圖8a和圖8b的仿真波形分別顯示出低帶寬探頭對目標信號過沖幅度的抑制作用和對目標信號尖刺波形的平滑作用。

綜上所述本節(jié)的分析得到以下主要結論:

（1）電壓探頭對目標信號的負載效應和測量系統(tǒng)與目標信號的級聯效應共同導致上升時間的測量誤差，且誤差隨探頭的輸入電容或上升時間增大而增大。

（2）電壓探頭的帶寬和上升時間成反比。

（3）電壓探頭帶寬過低將使測得信號的過沖幅度下降、尖刺波形平滑。

寄生電感

為了提高測量的靈活性，高阻無源探頭的地線端通常設計為拖尾的鱷魚夾，引入了地線線路電感和接地環(huán)路電感。出于同樣的原因，有源高壓差分探頭的信號端通常留有一定長度的引線，于是也引入了寄生電感。此外，有些探測點受限于物理空間而難以直接測量，通常需要在探測點和探頭間額外接入一段引線，這同樣會引入寄生電感。

探頭前端的寄生電感Lp與輸入電容Ci相互影響，兩者在高頻時形成諧振，諧振頻率為

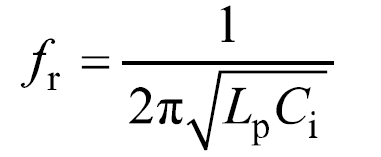
對于某一確定的探頭，其諧振頻率將隨寄生電感的增大而減小。考慮到諧振頻率附近，電壓探頭增益劇增,因此當諧振頻率靠近或低于探頭帶寬時，探頭在帶寬內的線性度將極大降低。

當目標信號有過沖或振鈴現象時，探頭前端的寄生電感會加劇目標信號測量結果的振蕩。不同探頭寄生電感下VDs2和VGs2的仿真波形比較如圖9所示。以VDs2的上升暫態(tài)波形為例進行分析，由圖9a可知其振鈴階段的振蕩頻率約為100MHz。

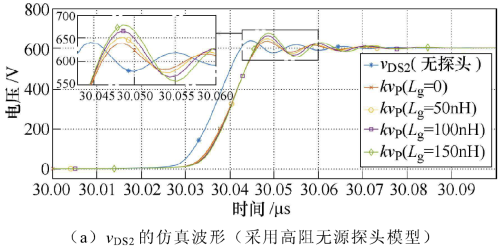
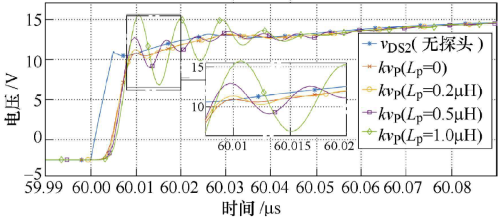
圖9. 不同探頭寄生電感下VDs2和VGs2的仿真波形比較

仿真所用無源探頭的輸入電容為 9.5pF，取地線電感Lg分別為50nH、100nH、150nH，則探頭的諧振頻率依次約為230MHz、160MHz、130MHz。可知，隨著地線電感增大，諧振頻率逐漸接近于目標信號振蕩頻率，這將導致探頭對振蕩頻率附近分量的增益變大。如圖9a 所示，隨著地線電感增大，VDs2測量結果的過沖幅度漸次增大，這與分析一致。

即使目標信號無明顯過沖現象，當電壓探頭的諧振頻率接近或低于目標信號的拐點頻率時，測量結果仍會出現過沖或振鈴，圖9b即為這種情況。

綜上所，本節(jié)的分析得到以下主要結論:

（1）電壓探頭的寄生電感與輸入電容對目標信號高頻分量產生諧振作用，諧振頻率隨寄生電感的增大而降低。

（2）當電壓探頭諧振頻率逐漸降低且逼近于目標信號振蕩頻率時，測得波形的振蕩幅度將增大。

（3）低諧振頻率電壓探頭對無明顯過沖現象的目標信號仍能產生振蕩作用。

共模抑制比

對于差分探頭，其輸出電壓可表示為

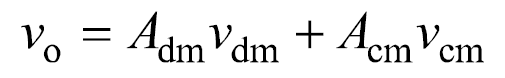
式中，Vdm與Vcm分別為輸入電壓信號的差模分量和共模分量。由式(1)可得

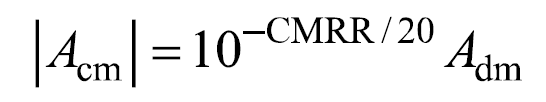
如果取共模增益極性為正，則有

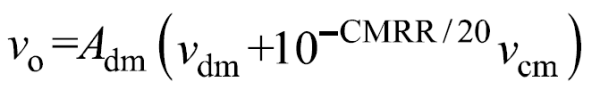
進而可定義差分探頭輸入信號的偽差模分量為

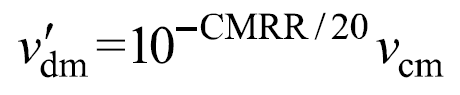
偽差模分量與差模分量的比值衡量了差分探頭的“共模誤差”，即

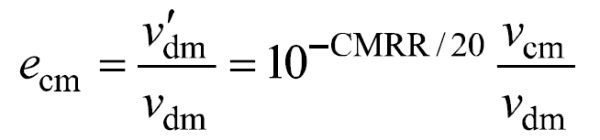
由于差分探頭兩差分信號路徑的阻抗對稱性隨頻率增大而變差，因此差分探頭的共模抑制比一般隨共模分量頻率增大而降低。對于具有相同差模分量幅度和共模分量幅度的信號，差分探頭的“共模誤差”將隨信號頻率升高而顯著增大。

差分探頭在低于帶寬時的差模增益基本不變，約為其衰減系數的倒數，即有kAdm≈1，因此差分探頭的數據表中一般用201g(k|Acm|)表示共模抑制比，它與式(1)中定義的共模抑制比近似互為相反數。不同的探頭共模抑制比下VGs1的仿真波形比較如圖10所示。圖10a為典型有源高壓差分探頭“共模抑制比”的頻率響應曲線，為方便分析，仿真時取共模抑制比為常值，用這些共模抑制比不同的探頭測量VGs1，得到圖10b的仿真結果。仿真電路下管處于關斷狀態(tài)時，VGs1差模電壓為-3V，共模電壓約為600V。取共模抑制比為60dB的探頭分析，由式(17)可算出該探頭輸入信號的偽差模分量為0.6V，進而由式(18)可得該探頭測量結果的“共模誤差”達到20%，這與仿真結果一致。此外，由仿真波形可知，隨著共模抑制比的提高，探頭的“共模誤差”逐漸減小。

綜上所述本節(jié)的分析得到以下主要結論:

（1）“共模誤差”由兩個因素組成：

①差分探頭的共模抑制比；

②目標信號的共模分量與差模分量之比，且“共模誤差”隨前者的增大或后者的減小而減小。

（2）差分探頭的共模抑制比一般隨共模分量頻率增大而減小，這導致開關器件暫態(tài)信號的“共模誤差”往往比穩(wěn)態(tài)信號的“共模誤差”更大。

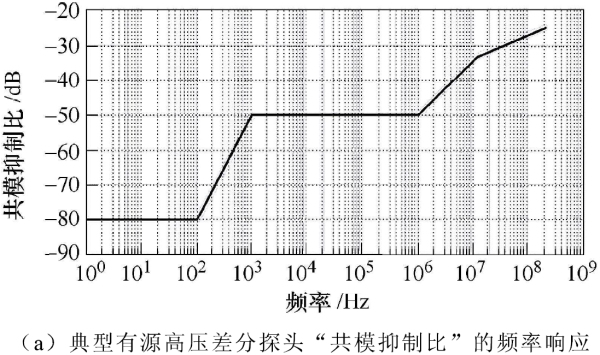
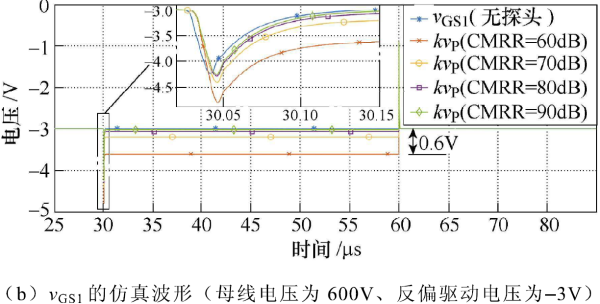
圖10. 不同的探頭共模抑制比下VGS1的仿真波形比較