YOKOGAWA的功率分析儀有一個Delta功能，該功能簡單來說就是通過測量的三相線電壓計算三相相電壓，反過來如果是3P4W接法，就是通過三相相電壓計算出線電壓的值。

   收到客戶關于該功能計算是否正確的疑問，因此覺得有必要就三相矢量運算做個簡單的說明。

無論是電工原理的描述還是在眾多工程師的觀念里，三相線電壓與相電壓的關系就是√3≈1.732，例如線電壓380V，那么相電壓就等于380V÷√3≈220V。這種簡單的估算方法很多情況下是成立的、有效的。言中之意：使用1.732作為運算系數只能在大部分的情況下作為估算的手段，而并不是真正意義的嚴格算法。

   為了說明上述的觀點，我們首先要解釋一下，√3的由來。

   必須假定三相電壓是平衡電路，所謂的平衡指的是三相相電壓夾角互為120°，三相電壓的矢量幅值完全相等（如下圖）。

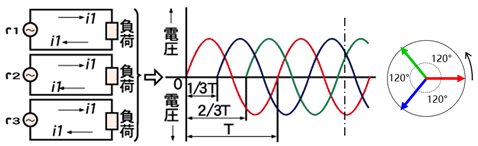
   假定了三相電壓平衡的前提后，我們就可以進行如下圖的矢量運算：

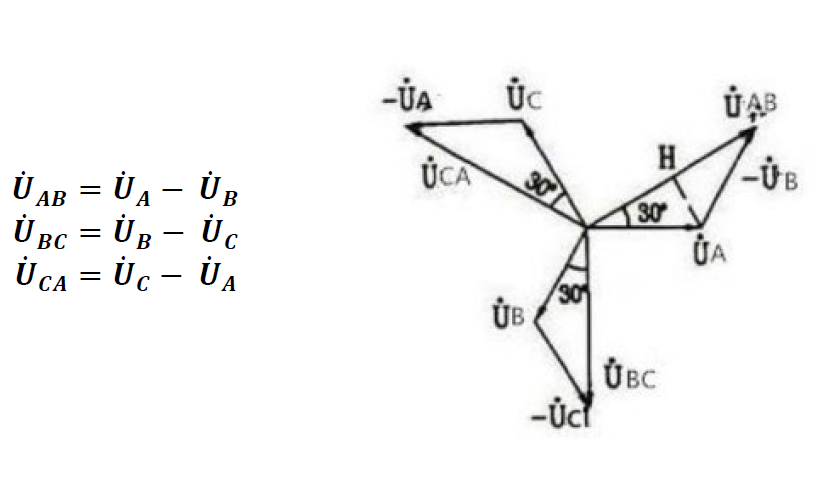
    然后按照三角形計算（等腰三角形，頂角120°，底角30°）通過三角函數運算即可以得出線電壓是相電壓的√3倍，同理其他兩相也是這個關系。

   從這個計算可以清晰看到，如果三個相位角120°，三相矢量幅值有任意一個不同，圖形就不可能是等腰三角形，換而言之√3的關系也不存在了。因此我們在利用√3作為換算系數在大多數場合都是可行的，但如果三相電壓矢量偏差較大，就不能用這種簡易算法。

    而現實中，三相電壓不平衡是普遍存在的，此處且不討論三相電壓不平衡產生的原因，此文只針對不平衡情況下的矢量運算進行探討。 

    那么既然√3不能通用，橫河功率分析儀中的Delta功能是如何運算的呢？

    我們先討論Star→Delta的情況，即已知三相相電壓矢量幅值與三相電壓的夾角，求三相線電壓的值。在此處，假定三個相位角不相同，三個相電壓幅值也不同。

   雖然起始條件不同，但矢量運算法則還是一樣的：

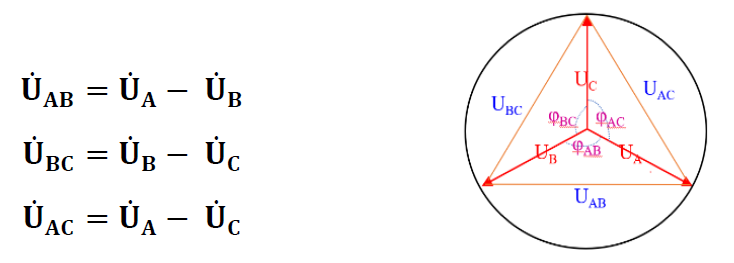
    這里既可以通過矢量運算來算出三相線電壓向量的模和角度，也可以通過簡單的三角函數運算直接算出UAC、UBC、UAB的值。

    已知兩邊長和頂角，利用余弦定理可得如下算式：

   當然如果將該圖形以圓心作為坐標原點直接代入四象直角坐標系，利用定位坐標的方法計算，只要算出每個向量的坐標值，剩下的就是簡單的坐標系運算，并且可以在坐標系中直接畫出線電壓向量（如下圖），至于計算過程此處不再詳述。

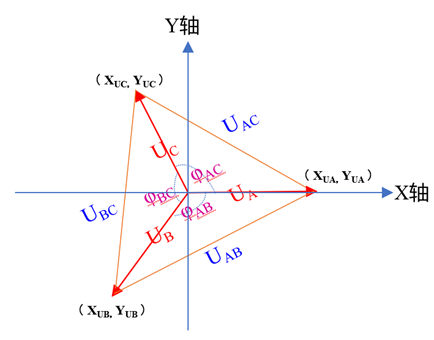
    上文中我們詳細說明了通過三個相電壓計算線電壓的原理和運算過程，那么反過來能否通過測量出來的線電壓算出相電壓呢？

   嚴格意義上的答案是“否定”的，理由如下：

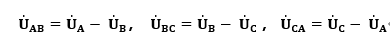
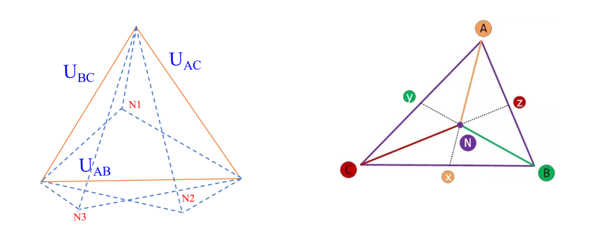
   那么如果增加個約束條件，根據對稱分量法，分解出零序電壓為零的前提下——

   (1)重心到頂點的距離與重心到對邊中點的距離之比為2:1。

   (2)重心坐標(XN,YN)是頂點坐標的平均數，即：

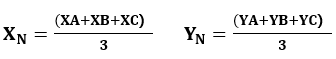
   (3)以重心為起點，以三角形三頂點為終點的三條向量之和等于零向量。

   性質(3)提到三個向量之和為零，其實就是“零序電壓為零”。

   既然確定了N點為三角形重心，那么三相電壓就可以用簡單三角形幾何關系推導出公式：

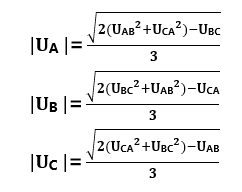
   總結

   通過簡單的幾何關系和三角函數運算我們可以進行Star→Delta運算；如果確定中性點在三角形重心，那么也可以直接通過測量線電壓計算相電壓。

   此外，留個伏筆，我們能否通過線電壓的相位關系計算出相電壓的相位差呢？答案是“OK”的。利用三角形余弦定理已知三邊長，可以輕松計算出三個夾角，有興趣的讀者可以自己算一下。

   本文并未涉及相電流的計算，如果加入相電流的向量，是否可以通過運算將3V3A測量出來的？線電壓/相電流以及電壓電流的相位關系轉化為相功率呢？此處省略10000字……O(∩_∩)O~。